Exercises: Tangent of a parabola

Wie gut kennst du dich mit Tangenten aus? Lerne mit diesen Aufgaben, die Tangentengleichung an Parabeln zu berechnen.
- 1
Berechne die Tangente an die Funktion durch den Punkt .
For this task you need the following basic knowledge: Tangente an Parabel berechnen
Ohne Ableitung
Setze die quadratische Funktion mit der allgemeinen Tangentengleichung gleich
Bringe alles auf eine Seite
Berechne die Diskriminante und setze sie gleich Null
Berechne mit Hilfe der Parabelgleichung den y-Wert von B
Setze B in die allgemeine Tangentengleichung ein
Löse nach t auf und setze in die Diskriminantengleichung ein
Löse nach m auf und setze in t ein
Stelle die Tangentengleichung auf
Mit Ableitung
Setze den x-Wert von B ein und erhalte m
Setze m und B in die Geradengleichung ein und erhalte t
Stelle die Tangentengleichung auf
- 2
Berechne die Tangente an die Funktion durch den Punkt .
For this task you need the following basic knowledge: Tangente an Parabel berechnen
Ohne Ableitung
Setze die quadratische Funktion mit der allgemeinen Tangentengleichung gleich
Bringe alles auf eine Seite
Berechne die Diskriminante und setze sie gleich Null
Berechne mit Hilfe der Parabelgleichung den y-Wert von B
Setze B in die allgemeine Tangentengleichung ein
Löse nach t auf und setze in die Diskriminantengleichung ein
Löse nach m auf und setze in t ein
Stelle die Tangentengleichung auf
Mit Ableitung
Setze den x-Wert von B ein und erhalte m
Berechne mit Hilfe der Parabelgleichung den y-Wert von B
Setze m und B in die Geradengleichung ein und erhalte t
Stelle die Tangentengleichung auf
- 3
Berechne die Tangente an die Funktion durch den Punkt .
For this task you need the following basic knowledge: Tangente an Parabel berechnen
Ohne Ableitung
Setze die quadratische Funktion mit der allgemeinen Tangentengleichung gleich
Bringe alles auf eine Seite
Berechne die Diskriminante und setze sie gleich Null
Berechne mit Hilfe der Parabelgleichung den y-Wert von B
Setze B in die allgemeine Tangentengleichung ein
Löse nach t auf und setze in die Diskriminantengleichung ein
Löse nach m auf (z. B. durch Faktorisieren mit Hilfe einer binomischen Formel )
Setze mundb in die allgemeine Tangentengleichung ein und löse nach t auf
Stelle die Tangentengleichung auf
Mit Ableitung
Setze den x-Wert von B ein und erhalte m
Berechne mit Hilfe der Parabelgleichung den y-Wert von B
Setze m und B in die Geradengleichung ein und erhalte t
Stelle die Tangentengleichung auf
- 4
Berechne die Tangente an die Funktion durch den Punkt .
For this task you need the following basic knowledge: Tangente an Parabel berechnen
Ohne Ableitung
Setze die quadratische Funktion mit der allgemeinen Tangentengleichung gleich
↓ Bringe alles auf eine Seite.
↓ Berechne die Diskriminante und setze sie gleich Null
Berechne mit Hilfe der Parabelgleichung den y-Wert von B
↓ Setze B in die allgemeine Tangentengleichung ein
Löse nach t auf und setze in die Diskriminantengleichung ein
Löse nach m auf (z. B. durch Faktorisieren mit Hilfe einer binomischen Formel )
Setze m und b in die allgemeine Tangentengleichung ein und löse nach t auf
Stelle die Tangentengleichung auf
Mit Ableitung
Setze den x-Wert von B ein und erhalte m
Berechne mit Hilfe der Parabelgleichung den y-Wert von B
Setze m und B in die Geradengleichung ein und erhalte t
Stelle die Tangentengleichung auf
- 5
Berechne die Tangente an die Funktion durch den Punkt .
For this task you need the following basic knowledge: Tangente an eine Parabel berechnen
Ohne Ableitung
Setze die quadratische Funktion mit der allgemeinen Tangentengleichung gleich
↓ Bringe alles auf eine Seite.
Berechne die Diskriminante und setze sie gleich Null.
Berechne mit Hilfe der Parabelgleichung den y-Wert von B:
Setze m und B in die allgemeine Tangentengleichung ein:
Löse nach t auf und setze in die Diskriminantengleichung ein.
↓ Löse nach m auf (z. B. durch Faktorisieren mit Hilfe einer binomischen Formel ).
Setze m und B in die allgemeine Tangentengleichung ein und löse nach t auf.
Stelle die Tangentengleichung auf.
Mit Ableitung
Berechne mit Hilfe der Parabelgleichung den y-Wert von B:
Setze m und B in die Geradengleichung ein und erhalte t
Stelle die Tangentengleichung auf
- 6
Berechne die Tangente an die Funktion durch den Punkt .
For this task you need the following basic knowledge: Tangenten an Parabeln
Ohne Ableitung
Berechne als erstes mit Hilfe der Parabelgleichung den y-Wert von B, indem du in h einsetzt:
Setze nun die quadratische Funktion mit der allgemeinen Tangentengleichung gleich:
↓ Bringe alles auf eine Seite
Berechne die Diskriminante und setze sie gleich Null. Benutze beim Berechnen die zweite binomische Formel und multipliziere aus:
Setze B in die allgemeine Tangentengleichung ein und löse nach t auf:
Setze t jetzt in die Diskriminantengleichung ein:
↓ Multipliziere die linke Seite aus
↓ Verwende die binomische Formel
Setze m und B jetzt noch in die allgemeine Tangentengleichung ein und löse nach t auf:
Stelle die Tangentengleichung auf:
Mit Ableitung
Setze den x-Wert von B ein und erhalte m
Berechne mit Hilfe der Parabelgleichung den y-Wert von B:
Setze m und B in die Geradengleichung ein und erhalte t
Stelle die Tangentengleichung auf
- 7
Berechne die Tangente an die Funktion durch den Punkt .
For this task you need the following basic knowledge: Tangente an Parabeln berechnen
Ohne Ableitung
Multipliziere mit Hilfe der binomischen Formel aus
Setze die quadratische Funktion mit der allgemeinen Tangentengleichung gleich
Bringe alles auf eine Seite
Berechne die Diskriminante und setze sie gleich Null
Berechne mit Hilfe der Parabelgleichung den y-Wert von B
Setze B in die allgemeine Tangentengleichung ein
Löse nach t auf und setze in die Diskriminantengleichung ein
Löse nach m auf (z. B. durch Faktorisieren mit Hilfe einer binomischen Formel )
Setze m und b in die allgemeine Tangentengleichung ein und löse nach t auf
Stelle die Tangentengleichung auf
Mit Ableitung
Setze den x-Wert von B ein und erhalte m
Berechne mit Hilfe der Parabelgleichung den y-Wert von B
Setze m und B in die Geradengleichung ein und erhalte t
Stelle die Tangentengleichung auf
- 8
Berechne den Berührpunkt und die Gleichung einer Tangente an die Parabel so, dass die Tangente zur Tangente im Berührpunkt senkrecht ist.
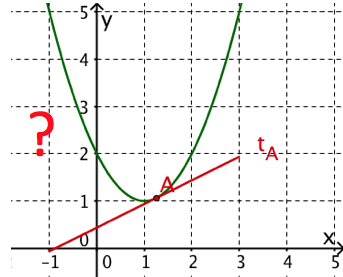
For this task you need the following basic knowledge: Tangenten an Parabeln berechnen
Die Tangente an einer Parabel ist eine Gerade, welche die Parabel in einem Punkt berührt und deren Steigung der Ableitungswert der Parabel im Berührpunkt ist.
Gegeben:
und
Gesucht:
Parabelpunkt
Berechne die 2. Koordinate von durch Einsetzen in die Parabelgleichung.
Berechne die Ableitung und damit die Steigung der Tangente im Punkt .
↓ Einsetzen des Wertes
Für die zu senkrechte Steigung gilt: .
Setze den Steigungswert für ein und berechne die x-Koordinate des gesuchten Punktes
↓ Einsetzten von -2
Setze in die Parabelgleichung ein, um zu erhalten.
Stelle die Tangentengleichung in auf.
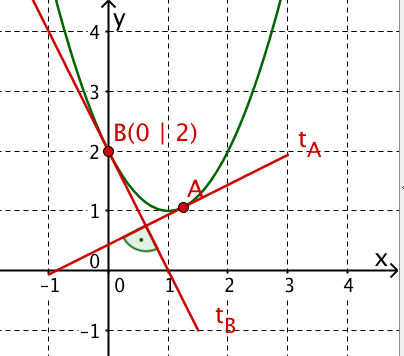
- 9
Die Tangenten von einem Punkt der Symmetrieachse der Parabel an die Parabel stehen aufeinander senkrecht. Berechne die Berührpunkte und die Gleichungen der Tangenten.
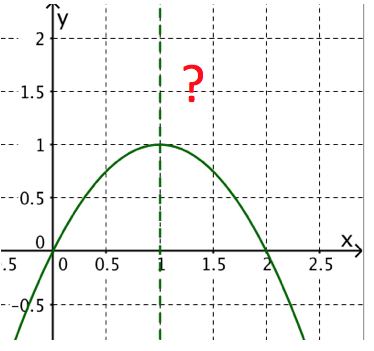
For this task you need the following basic knowledge: Tangentenberechnung
Entnimm der Scheitelpunktsform den Scheitelpunkt und die Symmetrieachse der Parabel.
ist Symmetrieachse
Wähle auf der Symmetrieachse einen beliebigen Punkt.
sei ein beliebiger Punkt auf der Symmetrieachse.
Stelle eine Geradengleichung durch den Punkt mit variabler Steigung auf.
Schneide die Gerade mit der Parabel durch Gleichsetzen der Funktionsterme.
↓ Löse die Klammer auf.
↓ Fasse zusammen
Damit die Gerade eine Tangente an die Parabel ist, dürfen sie nur einen gemeinsamen Schnittpunkt haben. In diesem Fall muss die Diskriminante der quadratischen Gleichung gleich null sein.
Setze die Diskriminante der quadratischen Gleichung
gleich null.
↓ Löse nach auf.
↓ Klammere aus.
Beachte jetzt die gestellte Aufgabe:
Die beiden Tangenten für bzw. sollen aufeinander senkrecht stehen.
Es muss also gelten:
Mit folgt .
Setze in
und .
Gib die Tangentengleichungen an.
Schneide die Tangenten mit der Parabel durch Gleichsetzen der Funktionsterme.
↓ Klammer auflösen.
↓ Fasse mit binomischer Formel zusammen.
↓ Die quadratische Gleichung hat nur eine Lösung.
Setze in ein:
↓ Fasse mit binomischer Formel zusammen.
↓ Die quadratische Gleichung hat nur eine Lösung.
Setze in ein: